BVH (Biovision Hierarchy) 構造仕様とモーションデータのワールド座標への変換

2024年8月3日2024年8月6日

BVH（Biovision Hierarchy）は、3Dアニメーションやモーションキャプチャーデータのフォーマットとして広く使用されるファイル形式です。BVHは、ボーン階層（ヒエラルキー）の構造と、各ボーンの動きを時間軸に沿って記録するデータの2つの部分から成り立っています。

BVHフォーマットの構造

BVHファイルはテキスト形式で、主に2つのセクションで構成されています。

ヒエラルキー（Hierarchy）セクション
このセクションでは、骨格の構造を定義します。各ボーンの名称や親子関係、初期の位置が記述されます。
モーション（Motion）セクション
ここでは、各フレームごとに各ボーンの位置や回転情報が記録されます。

BVH（Biovision Hierarchy）フォーマットのキーワードについて、各用語を説明します。

HIERARCHY

HIERARCHYセクションは、BVHファイルの最初の部分で、キャラクターの骨格構造（ボーンの階層）を定義します。

ここでは、ROOT、JOINT、End Siteがどのように繋がっているか、各ボーンがどのように配置されているかを指定します。
階層構造は波括弧 {} で囲まれ、ネストされた形で記述されます。

OFFSET

OFFSET は、各ボーン（ノード）が親ボーンからどれだけ離れているかを示す相対的な位置を指定します。

値は3つの浮動小数点数で、X、Y、Zの各軸方向のオフセットを示します。
例: OFFSET 0.00 10.00 0.00 は、親ボーンからX軸方向に0、Y軸方向に10、Z軸方向に0の位置にあることを意味します。

CHANNEL

CHANNEL は、各ボーンに対してアニメーションデータがどのように適用されるかを指定します。

各ボーンには、1つ以上のCHANNELが設定されます。
CHANNELS 6 Xposition Yposition Zposition Yrotation Xrotation Zrotationのように記述され、各ボーンの位置と回転の情報が指定されます。

CHANNELの種類:

Xposition, Yposition, Zposition: それぞれX、Y、Z軸に沿った平行移動を表します。これにより、ボーンが空間内でどの位置にあるかが決まります。
Yrotation, Xrotation, Zrotation: それぞれY、X、Z軸周りの回転を表します。これにより、ボーンがどの方向を向いているかが決まります。

ノードの種類

BVHファイルのヒエラルキーには、いくつかの基本的なノードの種類があります。

ROOT

ROOTは、ボーン階層の最上位に位置するノードです。このノードは、通常、キャラクターの中心となるボーン（例: Hip。
ROOTノードは、ワールド座標系の基点として機能し、すべての他のボーンがこのノードに対して相対的に位置づけられます。

JOINT

JOINTは、ROOTや他のJOINTに接続される子ノードです。通常、キャラクターの他のボディパーツ（例: Chest、Arm、Leg）を表します。
JOINTノードは、親ノードからの相対的な位置と回転を持ち、キャラクターのボーン構造を形成します。

End Site

End Siteは、ボーン階層の終端を示します。通常、手や足の先端などの末端部分に対応します。
End Siteは子ノードを持たず、単に階層の終了点を示します。

MOTION

MOTIONセクションは、BVHファイルの後半部分で、時間軸に沿ったアニメーションデータが格納されています。

このセクションには、FramesおよびFrame Timeに続いて、各フレームごとのチャンネルデータが記録されています。
例えば、各フレームにはXposition、Yposition、Zposition、Yrotation、Xrotation、Zrotationの値が続きます。
データはボーン階層の順序に従って、ルートボーンから順に記述されます。

Frames

Framesは、アニメーションデータの総フレーム数を示します。

例えば、Frames: 240と書かれていれば、240フレーム分のアニメーションデータがあることを意味します。
各フレームのデータが次のMOTIONセクションに続きます。

Frame Time

Frame Timeは、アニメーションデータが再生される速度を示す値です。

値は1フレームの時間（秒）で表されます。
例えば、Frame Time: 0.0333333 は、30FPS（1/30秒 = 約0.033秒）に相当します。

具体例

HIERARCHY
ROOT Hips
{
    OFFSET 0.00 0.00 0.00
    CHANNELS 6 Xposition Yposition Zposition Zrotation Xrotation Yrotation
    JOINT Chest
    {
        OFFSET 0.00 10.00 0.00
        CHANNELS 3 Zrotation Xrotation Yrotation
        End Site
        {
            OFFSET 0.00 10.00 0.00
        }
    }
}
MOTION
Frames: 2
Frame Time: 0.0333333
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00

HIERARCHYセクション:
ROOT Hips は骨格の基点（ルートボーン）です。
OFFSET 0.00 0.00 0.00 は、親ボーンからの相対的な位置を示します（この場合は原点）。
CHANNELS 6 は、このボーンが6つのチャンネル（3つの位置情報と3つの回転情報）を持つことを示します。
JOINT Chestは、「Hips」に接続された次のボーン（関節）です。
MOTIONセクション:
Frames: 2 は、2フレーム分のデータがあることを示します。
Frame Time: 0.0333333 は、各フレームの時間間隔（この場合は約30FPSに相当）を示します。
各フレームのデータは、それぞれのチャンネル（位置と回転）に対応する値のセットです。

3次元モーションデータをワールド座標に変換する方法

BVHファイルでは、各ボーンの位置と回転はその親ボーンに対する相対的なものです。このため、全体のキャラクターをワールド座標系で正しく位置づけるためには、各ボーンのローカル座標をワールド座標に変換する必要があります。

変換プロセス

ルートボーンの座標
ルートボーン（例: Hips）は、直接ワールド座標に配置されます。この座標が基準になります。
ボーンの階層構造に沿った変換
各子ボーンは親ボーンの座標系に依存しているため、まず親ボーンのワールド座標系での位置と回転を計算し、その上で子ボーンの相対的な位置と回転を加算します。

具体的には、次のステップで進めます：

各ボーンのローカル座標をその親ボーンのワールド座標に基づいて回転・平行移動し、ワールド座標を算出します。
この手順を階層の最下層まで繰り返します。

最終的なポジション
全てのボーンに対して、この変換を実行することで、キャラクターの全体的な動きがワールド座標系で表現されます。

具体例

https://github.com/Wasserwecken/bvhio/blob/main/bvhio/tests/example.bvh

HIERARCHY
ROOT Hips
{
	OFFSET	0.00	0.00	0.00
	CHANNELS 6 Xposition Yposition Zposition Zrotation Xrotation Yrotation
	JOINT Chest
	{
		OFFSET	 0.00	 5.21	 0.00
		CHANNELS 3 Zrotation Xrotation Yrotation
		JOINT Neck
		{
			OFFSET	 0.00	 18.65	 0.00
			CHANNELS 3 Zrotation Xrotation Yrotation
			JOINT Head
			{
				OFFSET	 0.00	 5.45	 0.00
				CHANNELS 3 Zrotation Xrotation Yrotation
				End Site 
				{
					OFFSET	 0.00	 3.87	 0.00
				}
			}
		}
		JOINT LeftCollar
		{
			OFFSET	 1.12	 16.23	 1.87
			CHANNELS 3 Zrotation Xrotation Yrotation
			JOINT LeftUpArm
			{
				OFFSET	 5.54	 0.00	 0.00
				CHANNELS 3 Zrotation Xrotation Yrotation
				JOINT LeftLowArm
				{
					OFFSET	 0.00	-11.96	 0.00
					CHANNELS 3 Zrotation Xrotation Yrotation
					JOINT LeftHand
					{
						OFFSET	 0.00	-9.93	 0.00
						CHANNELS 3 Zrotation Xrotation Yrotation
						End Site 
						{
							OFFSET	 0.00	-7.00	 0.00
						}
					}
				}
			}
		}
		JOINT RightCollar
		{
			OFFSET	-1.12	 16.23	 1.87
			CHANNELS 3 Zrotation Xrotation Yrotation
			JOINT RightUpArm
			{
				OFFSET	-6.07	 0.00	 0.00
				CHANNELS 3 Zrotation Xrotation Yrotation
				JOINT RightLowArm
				{
					OFFSET	 0.00	-11.82	 0.00
					CHANNELS 3 Zrotation Xrotation Yrotation
					JOINT RightHand
					{
						OFFSET	 0.00	-10.65	 0.00
						CHANNELS 3 Zrotation Xrotation Yrotation
						End Site 
						{
							OFFSET	 0.00	-7.00	 0.00
						}
					}
				}
			}
		}
	}
	JOINT LeftUpLeg
	{
		OFFSET	 3.91	 0.00	 0.00
		CHANNELS 3 Zrotation Xrotation Yrotation
		JOINT LeftLowLeg
		{
			OFFSET	 0.00	-18.34	 0.00
			CHANNELS 3 Zrotation Xrotation Yrotation
			JOINT LeftFoot
			{
				OFFSET	 0.00	-17.37	 0.00
				CHANNELS 3 Zrotation Xrotation Yrotation
				End Site 
				{
					OFFSET	 0.00	-3.46	 0.00
				}
			}
		}
	}
	JOINT RightUpLeg
	{
		OFFSET	-3.91	 0.00	 0.00
		CHANNELS 3 Zrotation Xrotation Yrotation
		JOINT RightLowLeg
		{
			OFFSET	 0.00	-17.63	 0.00
			CHANNELS 3 Zrotation Xrotation Yrotation
			JOINT RightFoot
			{
				OFFSET	 0.00	-17.14	 0.00
				CHANNELS 3 Zrotation Xrotation Yrotation
				End Site 
				{
					OFFSET	 0.00	-3.75	 0.00
				}
			}
		}
	}
}
MOTION
Frames:    2
Frame Time: 0.033333
 8.03	 35.01	 88.36	-3.41	 14.78	-164.35	 13.09	 40.30	-24.60	 7.88	 43.80	 0.00	-3.61	-41.45	 5.82	 10.08	 0.00	 10.21	 97.95	-23.53	-2.14	-101.86	-80.77	-98.91	 0.69	 0.03	 0.00	-14.04	 0.00	-10.50	-85.52	-13.72	-102.93	 61.91	-61.18	 65.18	-1.57	 0.69	 0.02	 15.00	 22.78	-5.92	 14.93	 49.99	 6.60	 0.00	-1.14	 0.00	-16.58	-10.51	-3.11	 15.38	 52.66	-21.80	 0.00	-23.95	 0.00	
 7.81	 35.10	 86.47	-3.78	 12.94	-166.97	 12.64	 42.57	-22.34	 7.67	 43.61	 0.00	-4.23	-41.41	 4.89	 19.10	 0.00	 4.16	 93.12	-9.69	-9.43	 132.67	-81.86	 136.80	 0.70	 0.37	 0.00	-8.62	 0.00	-21.82	-87.31	-27.57	-100.09	 56.17	-61.56	 58.72	-1.63	 0.95	 0.03	 13.16	 15.44	-3.56	 7.97	 59.29	 4.97	 0.00	 1.64	 0.00	-17.18	-10.02	-3.08	 13.56	 53.38	-18.07	 0.00	-25.93	 0.00

このBVHファイルのChest（胸部）のモーションデータをワールド座標系に変換する手順を説明します。この場合、まずローカル座標系のデータ（Chestの回転情報）を元にワールド座標系への変換を行います。

BVH構造の確認

まず、Chestの構造を確認します。

Chestは、Hipsからオフセット (0.00, 5.21, 0.00) の位置にあります。
Chestのモーションデータは、Zrotation Xrotation Yrotationの順に定義されています。
Hipsのモーションデータは、ワールド座標での位置 (Xposition Yposition Zposition) と回転 (Zrotation Xrotation Yrotation) の情報を持っています。

手順 1: Hipsのワールド座標系における変換

まず、Hipsの位置と回転を元にワールド座標系での変換を行います。

例として、最初のフレームのデータを使います。

Hipsの位置は (8.03, 35.01, 88.36) です。
Hipsの回転は (-3.41, 14.78, -164.35)（順序は Zrotation Xrotation Yrotation）です。

手順 2: Chestのローカル座標を変換

次に、Chestの回転データ (13.09, 40.30, -24.60) をHipsの回転に従ってワールド座標に変換します。

まず、Chestのオフセット (0.00, 5.21, 0.00) を考慮します。これをローカル座標系での回転行列を使って回転させ、その後Hipsの回転を適用します。

回転行列の適用

ここで、回転行列を順次適用します。3Dでの回転は行列計算が必要ですが、ここでは要点を簡略化して説明します。

Hipsの回転を適用:

Hipsの回転を反映した行列を計算します。回転行列の順序はZ, X, Yの順です。

Chestの回転を適用:

Chestの回転行列を計算し、Hipsの回転行列に掛け算します。

Chestのオフセットを回転:

回転されたオフセットを、Hipsの位置に加算します。

手順 3: ワールド座標への変換

この回転と平行移動を考慮した結果、最終的にChestのワールド座標系での位置を求めます。

具体的な計算

数式を使って具体的に計算すると、まず回転行列を計算し、それにChestのオフセットを掛けた後、Hipsの位置に加えます。

例えば、HipsのZ軸回転行列 Rz は以下のように計算します:

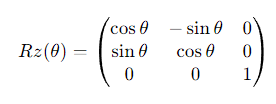
これをX軸、Y軸に対しても同様に行い、最終的にそれぞれの行列を掛け合わせます。そして、この結果にChestのオフセットを掛けて、最終的なワールド座標を得ます。

Pythonによる実装

もし、これを実際にPythonで実装する場合、次のようにして計算します:

import numpy as np

# 関数定義
def rotation_matrix(angles):
    z, x, y = np.deg2rad(angles)
    Rz = np.array([
        [np.cos(z), -np.sin(z), 0],
        [np.sin(z), np.cos(z), 0],
        [0, 0, 1]
    ])
    Rx = np.array([
        [1, 0, 0],
        [0, np.cos(x), -np.sin(x)],
        [0, np.sin(x), np.cos(x)]
    ])
    Ry = np.array([
        [np.cos(y), 0, np.sin(y)],
        [0, 1, 0],
        [-np.sin(y), 0, np.cos(y)]
    ])
    return Rz @ Rx @ Ry

# HipsとChestのデータ
hips_position = np.array([8.03, 35.01, 88.36])
hips_rotation = [-3.41, 14.78, -164.35]
chest_offset = np.array([0.00, 5.21, 0.00])
chest_rotation = [13.09, 40.30, -24.60]

# 回転行列を計算
hips_rotation_matrix = rotation_matrix(hips_rotation)
chest_rotation_matrix = rotation_matrix(chest_rotation)

# Chestのオフセットをローカル回転
chest_offset_rotated = hips_rotation_matrix @ chest_offset

# ワールド座標での位置を計算
chest_world_position = hips_position + chest_offset_rotated

print("Chestのワールド座標:", chest_world_position)

このコードでは、Hipsの位置と回転を反映した後、Chestのワールド座標系での位置を計算しています。

Chestのワールド座標: [ 8.3296403  40.03869482 89.68911402]

bvhio

これを使うとワールド座標への変換などが簡単にできるようになります

vec3(      8.32964,      40.0387,      89.6891 ) vec3(    0.0481175,     0.852046,    -0.521251 ) Chest

bvhio · PyPI

import bvhio
root = bvhio.readAsHierarchy('bvhio/tests/example.bvh')
root.printTree()

# load rest pose and print data
root.loadRestPose(recursive=True)
print('\nRest pose position and Y-direction of each joint in world space ')
for joint, index, depth in root.layout():
    print(f'{joint.PositionWorld} {joint.UpWorld} {joint.Name}')
# Set all joints to the first keyframe.
# The animation pose is calculated by -> Pose = RestPose + Keyframe.
root.loadPose(0)

# print info
print('\nPosition and Y-direction of each joint in world space ')
for joint, index, depth in root.layout():
    print(f'{joint.PositionWorld} {joint.UpWorld} {joint.Name}')

Hips
+- Chest
|  +- Neck
|  |  +- Head
|  +- LeftCollar
|  |  +- LeftUpArm
|  |     +- LeftLowArm
|  |        +- LeftHand
|  +- RightCollar
|     +- RightUpArm
|        +- RightLowArm
|           +- RightHand
+- LeftUpLeg
|  +- LeftLowLeg
|     +- LeftFoot
+- RightUpLeg
   +- RightLowLeg
      +- RightFoot

Rest pose position and Y-direction of each joint in world space 
vec3(            0,            0,            0 ) vec3(            0,            1,            0 ) Hips
vec3(            0,         5.21,            0 ) vec3(            0,     0.997333,    0.0729792 ) Chest
vec3(            0,        23.86,  1.19209e-07 ) vec3(            0,            1,            0 ) Neck
vec3(            0,        29.31,  1.19209e-07 ) vec3(            0,            1,            0 ) Head
vec3(         1.12,        21.44,         1.87 ) vec3(            1,  5.96046e-08,            0 ) LeftCollar
vec3(         6.66,        21.44,         1.87 ) vec3(            0,           -1,            0 ) LeftUpArm
vec3(         6.66,         9.48,         1.87 ) vec3(            0,           -1,            0 ) LeftLowArm
vec3(         6.66,    -0.450002,         1.87 ) vec3(            0,           -1,            0 ) LeftHand
vec3(        -1.12,        21.44,         1.87 ) vec3(           -1,  5.96046e-08,            0 ) RightCollar
vec3(        -7.19,        21.44,         1.87 ) vec3(            0,           -1,            0 ) RightUpArm
vec3(        -7.19,         9.62,         1.87 ) vec3(            0,           -1,            0 ) RightLowArm
vec3(        -7.19,        -1.03,         1.87 ) vec3(            0,           -1,            0 ) RightHand
vec3(         3.91,            0,            0 ) vec3(            0,           -1,            0 ) LeftUpLeg
vec3(         3.91,       -18.34,            0 ) vec3(            0,           -1,            0 ) LeftLowLeg
vec3(         3.91,       -35.71,            0 ) vec3(            0,           -1,            0 ) LeftFoot
vec3(        -3.91,            0,            0 ) vec3(            0,           -1,            0 ) RightUpLeg
vec3(        -3.91,       -17.63,            0 ) vec3(            0,           -1,            0 ) RightLowLeg
vec3(        -3.91,       -34.77,            0 ) vec3(            0,           -1,            0 ) RightFoot

Position and Y-direction of each joint in world space 
vec3(         8.03,        35.01,        88.36 ) vec3(    0.0575125,     0.965201,     0.255108 ) Hips
vec3(      8.32964,      40.0387,      89.6891 ) vec3(    0.0481175,     0.852046,    -0.521251 ) Chest
vec3(      9.16411,       56.599,      81.1521 ) vec3(     0.163858,     0.314978,    -0.934847 ) Neck
vec3(      10.0571,      58.3157,      76.0571 ) vec3(     0.136333,     0.863658,    -0.485292 ) Head
vec3(      8.02774,      53.6106,      80.5308 ) vec3(    -0.967669,     0.251636,    0.0172419 ) LeftCollar
vec3(      2.66686,      55.0047,      80.6263 ) vec3(    -0.901112,     0.170623,    -0.398605 ) LeftUpArm
vec3(     -8.11043,      57.0454,       75.859 ) vec3(     0.212169,    -0.689802,    -0.692213 ) LeftLowArm
vec3(     -6.00359,      50.1956,      68.9853 ) vec3(      0.21588,    -0.681081,    -0.699661 ) LeftHand
vec3(      10.2629,      53.5708,      80.6721 ) vec3(     0.953783,     0.278612,      0.11258 ) RightCollar
vec3(      16.0524,       55.262,      81.3554 ) vec3(     0.992285,     0.105528,   -0.0650799 ) RightUpArm
vec3(      27.7812,      56.5094,      80.5862 ) vec3(     0.105734,     0.764633,    -0.635733 ) RightLowArm
vec3(      28.9073,      64.6527,      73.8156 ) vec3(     0.117056,     0.781042,    -0.613409 ) RightHand
vec3(      4.25561,      34.9653,      89.3799 ) vec3(    -0.182967,    -0.963474,     0.195551 ) LeftUpLeg
vec3(     0.900007,      17.2952,      92.9663 ) vec3(   -0.0743765,    -0.450022,     0.889915 ) LeftLowLeg
vec3(    -0.391913,      9.47834,      108.424 ) vec3(   -0.0859881,    -0.463928,      0.88169 ) LeftFoot
vec3(      11.8044,      35.0547,      87.3401 ) vec3(     0.170185,    -0.858689,    -0.483414 ) RightUpLeg
vec3(      14.8047,       19.916,      78.8176 ) vec3(     0.135822,     -0.89424,     0.426482 ) RightLowLeg
vec3(      17.1327,      4.58869,      86.1275 ) vec3(     0.188425,    -0.981787,    0.0242779 ) RightFoot